Developer Notes¶
The purpose of this document is to explain the inner workings of MachUpX for those who are developing it. Please update this as often as you can.
Numerical Lifting-Line Implementation¶
MachUpX solves the formulation of the numerical lifting-line equation presented in Reid A General Approach to Lifting-Line Theory, Applied to Wings with Sweep and Goates, et al. “A Practical Implementation of General Numerical Lifting-Line Theory”, AIAA SciTech Conference, 2020. This formulation differs somewhat from the original formulation by Phillips and Snyder. Most significantly, the formulation is generalized to allow multiple aircraft to be analyzed at once. MachUpX sets up and solves the lifting-line equation in Earth-fixed coordinates. Once the distribution of vortex strengths is obtained, the forces and moments are integrated then transformed to the body-fixed frame for each aircraft.
Multiple Aircraft¶
For the most part, MachUpX is ignorant of how many aircraft are in the scene. When performing calculations, it will simply execute a for loop on the stored dictionary of aircraft. I have made some exceptions to this to try to speed things up. The exceptions have mostly been made in instances where there are calculations which could be performed at both the scene or the aircraft leve. To speed things up, I’ve dropped the computations down to the aircraft level where possible.
API to Aircraft¶
When using MachUpX as a Python module, the Airplane class is never exposed to the user. Rather, the user calls getters and setters through the Scene class and supplies the name of the target aircraft to effect changes.
In the future, it could be beneficial to allow the user access to the Airplane class directly. The user could instantiate an aircraft object and then pass this object as an argument to the Scene constructor. This would require some kind of listener/binding between the Airplane class and the Scene class so that certain functions in the Scene class, such as _perform_geometry_calculations(), are called whenever a change is made to the Airplane object. This is just an idea.
Wing Segment Tree Structure¶
In implementing the WingSegment class, the set of wing segments constituting an airplane are stored as a tree. There is an origin segment, which has no properties. Other segments are then attached to (or more accurately, defined relative to) this segment. Each segment knows which segments are attached to it and segments are added recursively. This structural choice was motivated by two factors. For one, recursion is elegant, simple, and fast. The second is that this will more naturally allow for calculating the influence of forces and moments exerted by outboard wing segments on inboard segments. The tree can be traversed recursively and forces, moments, and aeroelastic deflections can be integrated as the function backs out of the recursion. Aeroelastic effects are not yet implemented in MachUpX and so this may change in the future as needed functionality becomes clearer.
Mean Aerodynamic Chord (MAC) Calculation¶
MAC seems to be a poor man’s estimate for the aerodynamic center, but not quite. It is based entirely off of geometry, no aerodynamics involved. I took information from the following to code this up:
- Raymer “Simplified Aircraft Design for Homebuilders”
- McCormick “Aerodynamics, Aeronautics, and Flight Mechanics”
- Nickel & Wohlfahrt “Tailless Aircraft in Theory and Practice”
- Phillips “Mechanics of Flight”
There is agreement between all sources on only one thing, the definition of the MAC as a reference length. This is given by Phillips Eq. 1.8.86 (excuse my ASCII math):
b/2
1 / 2
MAC = - | c dy
S /
-b/2
Phillips and Raymer are the only ones to tie the MAC to a specific location on the wing. Phillips simply states that there is a spanwise position on the wing where the local chord is equal to the MAC. Raymer also does this and presents a graphical method for determining the position of the MAC on a tapered wing. He briefly describes how to find the MAC for a compound tapered wing, stating the MAC should be found for each section separately and the the 25% point should be averaged using an area-weighted average. N&W and McCormick simply give the MAC as a reference length and give it no positional significance.
Raymer ties the MAC to an introductory discussion of stability. He states, “The MAC is a sort of averaged chord, and the entire wing tends to act as if all its area were concentrated at the MAC.” He thereby claims the point of neutral stability (i.e. the aerodynamic center) on the wing is at the 25% MAC location. He then recommends, for a tailed airplane, that the CG be placed at the 25% MAC location so the wing is neutrally stable and all longitudinal stability comes from the horizontal stabilizer. This is reasonable, given his assumptions.
Phillips directly disputes the assumption that the wing aerodynamic center lies on the MAC. He shows this is not true for most wing geometries (see Figure 1.8.28 in his book). However, he focuses on the fact that the aerodynamic center does not lie on the same spanwise position as the MAC. For an unswept wing, Phillips states the aerodynamic center of the wing lies on the locus of section aerodynamic centers (i.e. 25% root chord). This agrees with Raymer’s claim, as the 25% MAC location also lies on the straight locus of section aerodynamic centers. For swept wings, determining the location of the wing aerodynamic center becomes more hairy. Phillips gives the following approximation (Eq. 1.11.9):
/ b/2 \
_ 1 d | / ~ |
x = ---- -- | | CL c x dy |
ac CL,a da | / ac |
\-b/2 /
If we assume the section lift coefficient is constant over the span, as is often done, this reduces to:
b/2
_ 1 / ~
x = - | c x dy
ac S / ac
-b/2
This can be interpreted as an area-weighted average of the section aerodynamic centers. N&W provide this equation and call this the “C-Point” or “Center of Lift for Constant Local Lift Coefficient”. This makes sense. They then recommend the CG be placed at least 6-12% of the MAC in front of the C-Point for a flying wing. As the main wing constitutes the entire airframe of a flying wing, this is simply the recommendation that the aircraft have a static margin of at least 6-12%. Very reasonable.
I have coded up both methods of determining the main wing aerodynamic center (Raymer’s and Phillips’). For unswept wings, the 25% MAC location and the average of the section aerodynamic centers are the same, i.e. 0. For swept straight and tapered wings, they are also the same. For swept elliptic wings, however, the two results diverge. Therefore, I have decided that in MachUpX, calling Scene.MAC() will give you the MAC (that is, the reference length) and the location of the C-Point. This seems to me to be the most reliable.
Definition of Sideforce¶
Dr Hunsaker and Jaden Thurgood have done an excellent job of standardizing the directions of lift, drag, and sideforce for the AeroLab. However, their derivation relies on calculating trigonometric values, which is computationally expensive. MachUpX, instead, uses vector definitions, which are much faster to compute. All that is required is the freestream direction vector in body-fixed coordinates, u_inf. This defines the direction of drag. Taking the cross product of this with the body-fixed y-axis vector and normalizing gives us the lift direction vector, u_lift. To complete the system, the sideforce direction vector is given by the cross product of u_lift with u_inf. This should already be normalized, but it can be normalized again to make sure. The force vector in body-fixed coordinates can then simply be dotted with each of these direction vectors to obtain L, D, and S. Taking the dot product of a vector with a unit vector gives the projection of the first vector in the direction of the unit vector.
Differences in Implementation between MachUpX and MachUp Pro¶
Users will notice that differences exist between the results obtained from the two versions of MachUp. Here is a list of things which vary in the implementations and which will affect results.
- MachUpX allows Kuchemann’s LAC correction.
- MachUpX implements thin-airfoil theory corrections to swept section properties.
- MachUpX implements Reid’s horseshoe vortex geometry corrections (i.e. jointed vortices and effective LAC).
- MachUpX redimensionalizes section properties using the total (freestream plus induced) velocity at each control point. MachUp Pro uses only the freestream.
- MachUpX has a slightly different nonlinear Jacobian (a consequence of the above). This does not affect the final solution, only convergence rates.
- MachUpX defaults to clustering control points about flap edges.
- MachUpX uses CL_max to truncate section lift coefficients within the lifting-line algorithm. MachUp Pro only uses this to determine stall onset.
- MachUpX uses only the in-plane velocity for determining section behavior.
- MachUp Pro scales section coefficients by the magnitude of the freestream including rotation. MachUpX doesn’t need to do this.
All of these can be toggled in MachUpX by the user. Under the “grid” parameter for each wing, “reid_corrections” and “flap_edge_cluster” can be specified. Also, “ll_offset” can be set as “kuchemann” for each wing. In the input file under “solver”, “use_swept_sections”, “use_total_velocity”, “use_in_plane”, and “match_machup_pro” can be specified. “CL_max” is specified in the input for each airfoil.
A couple minor differences which cannot be toggled are:
- MachUpX uses the experimental sideslip angle whereas MachUp Pro uses the analytical sideslip angle.
- MachUpX uses a different definition for the directions of lift, drag, and sideforce. These are guaranteed to be orthogonal, whereas those given by MachUp Pro are not.
- MachUp Pro is an inherently nondimensional derivation which ignores increases in local freestream velocity due to aircraft rotation. At this point (June 2020), we have been unable to determine exactly how to alter the dimensional derivation in MachUpX to correct for this.
Correcting Section Properties for Sweep¶
Jackson’s original GNLL uses empirical fits of data he obtained from vortex panel method to correct airfoil sections for sweep. However, he did it such that the corrections for the moment coefficient apply to the moment about the leading edge. This is very inconvenient, especially when using “database” or “poly_fit” type airfoils. For this reason, MachUpX corrects the section coefficients using thin-airfoil theory. These corrections are summarized here (see Goates, et al. “A Practical Implementation of General Numerical Lifting-Line Theory”, AIAA SciTech Conference, 2020 for a more in-depth discussion).
- Zero-lift angle of attack is scaled by 1/cos(sweep).
- Section moment coefficient is scaled by 1/cos(sweep).
- Drag is weird…
Coordinate Systems¶
Throughout MachUpX, two coordinate systems are used. These are the body-fixed and earth-fixed coordinate systems. In the body-fixed coordinate system, the x-axis points forward out of the nose of the aircraft, the y-axis points to the right along the wing, and the z-axis points down. The body-fixed coordinate system has its origin at the aircraft’s center of gravity.
In the earth-fixed coordinate system, the x-axis points North, the y-axis points East, and the z-axis points down. The origin of the earth-fixed coordinate system is somewhat arbitrary, but it is assumed to be at sea level. In this coordinate system, the earth is assumed to be flat.
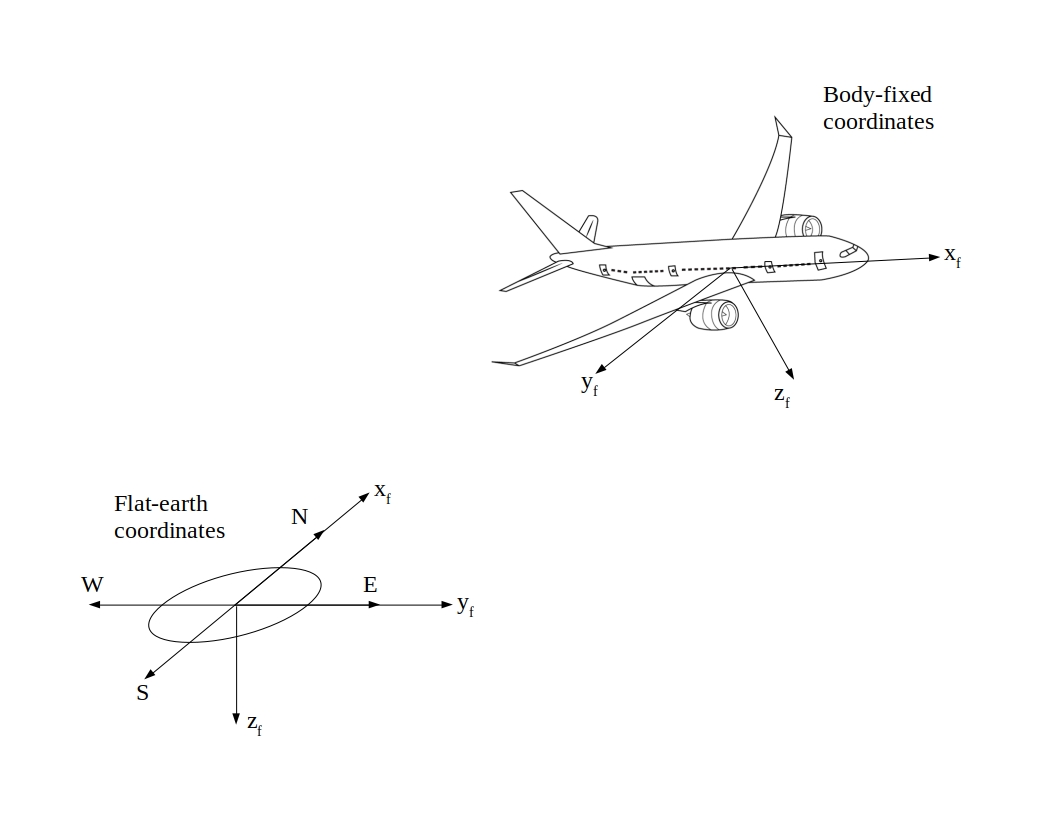
Calculations occurring within the Scene class are almost always done in the earth-fixed frame. Calculations occurring within the Airplane and WingSegment classes are done in the body-fixed frame.